Sparse Graph Optimization using Weighted Quantum Wires in Rydberg Atom Arrays
Overview
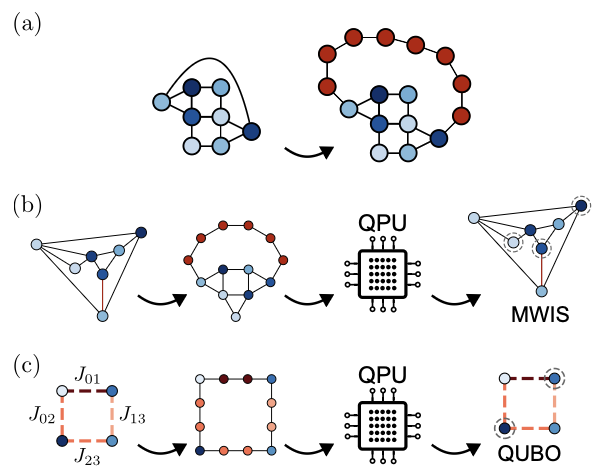
Neutral atom arrays provide a versatile platform to implement coherent quantum annealing as an approach to solving hard combinatorial optimization problems. In this work we present and experimentally demonstrate an efficient encoding scheme based on chains of Rydberg-blockaded atoms, which we call quantum wires, to natively embed maximum weighted independent set (MWIS) and quadratic unconstrained binary optimization (QUBO) problems on a neutral atom architecture. For graphs with quasi-unit-disk connectivity, in which only a few long-range edges are required, our approach requires a significantly lower overhead in the number of ancilla qubits than previous proposals, facilitating the implementation on currently available hardware. To demonstrate the approach, we perform weighted-graph annealing on a programmable atom array using local light shifts to encode problem-specific weights across graphs of varying sizes. This approach successfully identifies the solutions to the original MWIS and QUBO graph instances. Our work expands the operational toolkit of near-term neutral atom arrays, enhancing their potential for scalable quantum optimization. For more details see arXiv:2503.17115.
Weighted Quantum Wires
![Weighted Quantum Wires (a) Basic construction of a wire to connect two nodes with weights α and β in MWIS and QUBO problems. The energy diagram shows the ordering of the eigenstates for an MWIS implementation. (b, c) Wire constructions to delocalise triangular and all-to-all square interactions between vertices in MWIS problems. (d) Generalization of the crossing gadget introduced in [33] to allow for arbitrary weights of the nodes.](images/quantum-wires.png)
Weighted Quantum Wires (a) Basic construction of a wire to connect two nodes with weights α and β in MWIS and QUBO problems. The energy diagram shows the ordering of the eigenstates for an MWIS implementation. (b, c) Wire constructions to delocalise triangular and all-to-all square interactions between vertices in MWIS problems. (d) Generalization of the crossing gadget introduced in [33] to allow for arbitrary weights of the nodes.