Graph Colouring via Quantum Optimization on a Rydberg-Qudit Atom Array

Summary

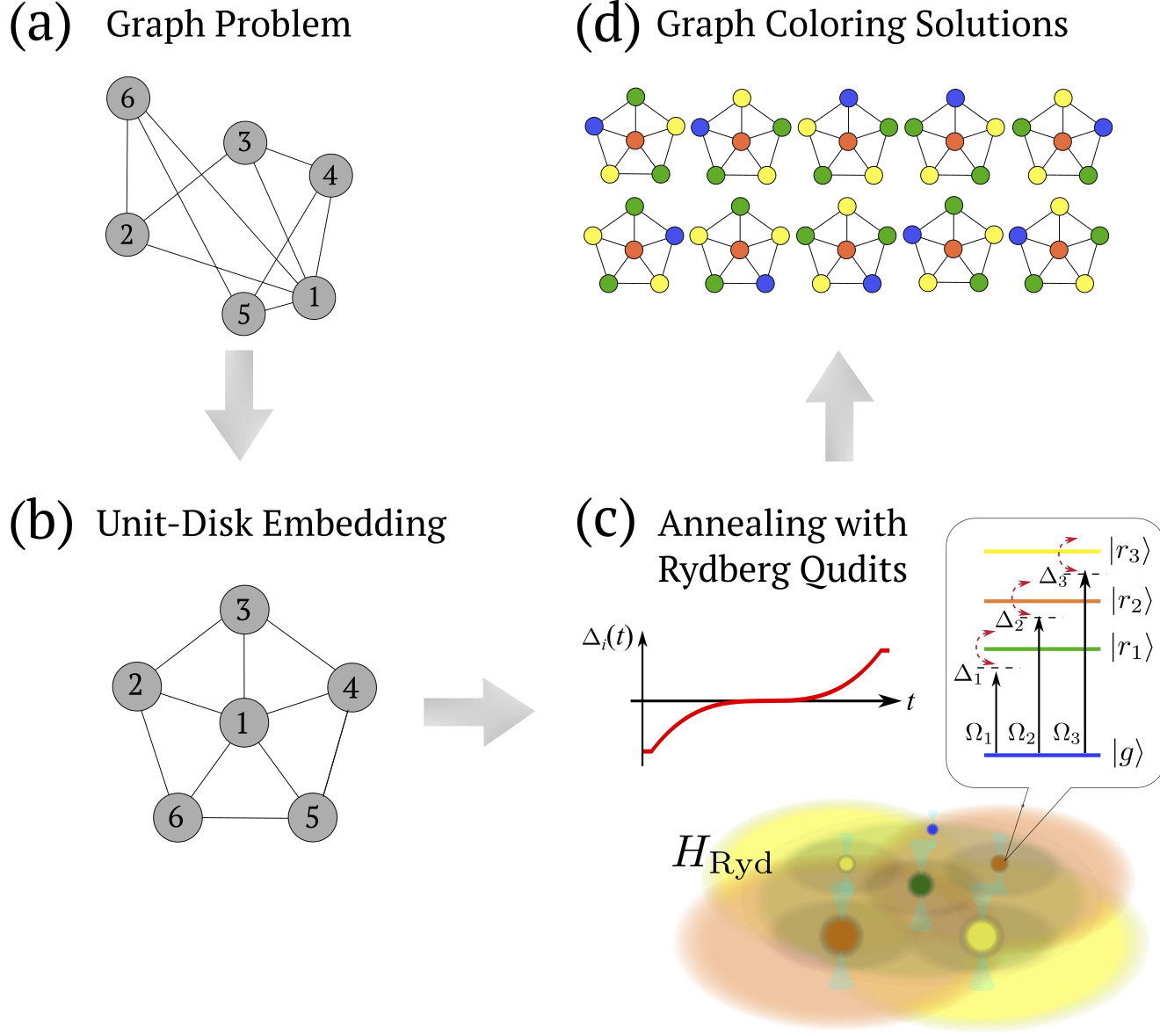
We propose a new approach to natively embedding graph colouring problems onto neutral atom arrays using multiple Rydberg states each representing a unique colour. Graph colouring arises in a wide range of industrially relevant optimisation problems from sharing data across a wifi network to scheduling tasks and planning workloads. Using multiple Rydberg states enables efficient encoding of this problem onto quantum hardware and provides a new direction for near-term applications of neutral atom quantum computing. For more details see arXiv.2504.08598.

Key Results

Neutral atom arrays have emerged as a versatile candidate for the embedding of hard classical optimization problems. Prior work has focused on mapping problems onto finding the maximum independent set of weighted or unweighted unit disk graphs. In this paper we introduce a new approach to solving natively-embedded vertex graph colouring problems by performing coherent annealing with Rydberg-qudit atoms, where different same-parity Rydberg levels represent a distinct label or colour. We demonstrate the ability to robustly find optimal graph colourings for chromatic numbers up to the number of distinct Rydberg states used, in our case k = 3. We analyse the impact of both the long-range potential tails and residual inter-state interactions, proposing encoding strategies that suppress errors in the resulting ground states. We discuss the experimental feasibility of this approach and propose extensions to solve higher chromatic number problems, providing a route towards direct solution of a wide range of real-world integer optimization problems using near-term neutral atom hardware. For more details see arXiv.2504.08598.