Demonstration of weighted graph optimization on a Rydberg atom array using local light-shifts
Demonstration of weighted graph optimization on a Rydberg atom array using local light-shifts

Demonstration of weighted graph optimization on a Rydberg atom array using local light-shifts

Apr 4, 2024

Overview

In this paper we present first demonstrations of weighted graph optimization on a Rydberg atom array using annealing with local light-shifts. We verify the ability to prepare weighted graphs in 1D and 2D arrays, including embedding a five vertex non-unit disk graph using nine physical qubits. We find common annealing ramps leading to preparation of the target ground state robustly over a substantial range of different graph weightings. This work provides a route to exploring large-scale optimization of non-planar weighted graphs relevant for solving relevant real-world problems. For more details see arXiv:2404.02658.

Graph Optimisation using Neutral Atom Arrays

Neutral atom arrays have emerged as a versatile platform towards scalable quantum computation and optimisation, capable of implementing high fidelity digital gates and logical qubit encodings with arbitrary connectivity [1], as well as enabling solution of classical optimisation problems using analogue quantum annealing [2]. Early demonstrations of solving the Maximum Independent Set (MIS) problem using arrays of up to 289 qubits found for hard problems the quantum hardware offered a speedup over classical solvers [3], however recent analysis shows for MIS problems on unit disk graphs improved classicalv solvers can find solutions for thousands of qubits [4].

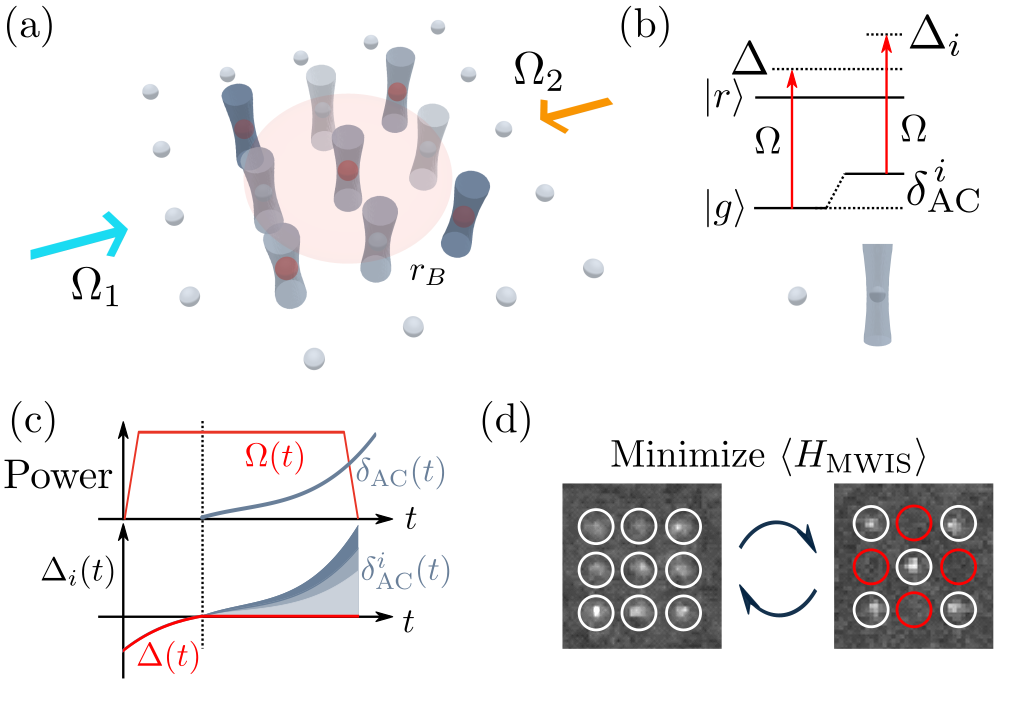
A recent proposal from Nguyen et al. [5] shows that by introducing local light-shifts it is possible to extend beyond solving MIS to a wide range of problems including maximum weighted indpendent set (MWIS), quadratic unconstrained binary optimisation (QUBO) and even factorisation with at worst a quadratic overhead in qubit number. This approach uses gadgets to map a given problem onto a unit-disk graph (UDG) MWIS with local light-shifts to implement weightings. In this work, we implement the first experimental demonstrations of UDG-MWIS optimisation using local light-shifts.

Local Light-shifts

To implement weighted graph annealing with local light-shifts we use an additional laser and spatial light modulator (SLM) to project a secondary tweezer array onto the atoms with a programmable relative power. This light-shift potential allows us to precisely control the relative weight on each qubit, whilst performing global control of the laser intensity to enable simplified annealing protocols with a finite number of parameters. For our Cs atoms the 800 nm light causes a blue-shift (positive detuning), so annealing ramps are performed using a two-stage process where the global Rydberg excitation lasers are first ramped to resonance, then the light-shift intensity shaped to give smoothly evolving light shifts on each site with fixed relative weighting to ensure the groundstate of the combined atom-light interaction encodes the solution to the classical UDG-MWIS problem.

Weighted 1D Chains

To verify the ability to use local light-shifts we begin with a simple example of a weighted 1D chain. Using uniform weighting, for an odd chain the blockade condition should ensure all atoms on odd sites are Rydberg excited. Introducing a relative weighting of 2 onto the even sites changes the resulting groundstate and causes the inverted case of Rydberg excitation on even sites. Below we show results of optimising the annealing for the weighted graph, and demonstrate the same annealing ramp is able to simultaneosuly prepare the groundstate of the uniformly weighted graph, demonstrating the ability to adiabatically preprare the groundstate of the system.

Optimisation with 1D weighted chains: (a) For a uniformly weighted, odd-length 1D graph the ground state is the Z2-ordered phase with Rydberg excitations on odd sites which corresponds to the unweighted MIS. Introducing a weighting with wi=2 on even sites results in an MWIS ground state with Rydberg excitations localized to the even sites which is no longer equivalent to the MIS solution. (b) Optimal annealing ramp for preparing the weighted ground state obtained via closed-loop optimization for N=9 atoms spaced by a=7 µm. Output state probability (c) and time evolution (d) for the unweighted graph showing the odd-ordered target ground state is prepared with 19(1)% probability. Output state probability (e) and time evolution (f) for the weighted graph showing even-ordered ground state is also prepared with 19(1)% probability.

Optimisation with 1D weighted chains: (a) For a uniformly weighted, odd-length 1D graph the ground state is the Z2-ordered phase with Rydberg excitations on odd sites which corresponds to the unweighted MIS. Introducing a weighting with wi=2 on even sites results in an MWIS ground state with Rydberg excitations localized to the even sites which is no longer equivalent to the MIS solution. (b) Optimal annealing ramp for preparing the weighted ground state obtained via closed-loop optimization for N=9 atoms spaced by a=7 µm. Output state probability (c) and time evolution (d) for the unweighted graph showing the odd-ordered target ground state is prepared with 19(1)% probability. Output state probability (e) and time evolution (f) for the weighted graph showing even-ordered ground state is also prepared with 19(1)% probability.

Weighted 2D Graphs

To demonstrate our ability to optimise for 2D graphs, we consider a simple 5-vertex weighted graph shown below, which can be mapped onto a UDG-MWIS graph with 9 atoms. We find annealing profiles that optimise this graph for the weightings (2,1,2,1,1) giving the correct groundstate solution as shown, and additionally find this same annealing profile works for a range of other weightings highlighting the versatiblity and robustness of the approach of using local light-shifts for solving graph optimisation problems.

Optimisation of a 2D weighted graph: (a) The target 5-vertex weighted graph problem is embedded into UDG-MWIS form for encoding onto a neutral atom array using 9 qubits, with 5 qubits encoding the vertices and 4 additional atoms required to implement the coupling of vertices 1 and 3 to vertex 5 whilst maintaining the constraint that no vertices connected by an edge can be simultaenously excited. (b) Result showing annealing of a weighted graph problem where the neutral atom hardware is able to correctly identify the solution corresponding to vertices 1 and 3 having higher weighting than 2, 4 and 5.

Optimisation of a 2D weighted graph: (a) The target 5-vertex weighted graph problem is embedded into UDG-MWIS form for encoding onto a neutral atom array using 9 qubits, with 5 qubits encoding the vertices and 4 additional atoms required to implement the coupling of vertices 1 and 3 to vertex 5 whilst maintaining the constraint that no vertices connected by an edge can be simultaenously excited. (b) Result showing annealing of a weighted graph problem where the neutral atom hardware is able to correctly identify the solution corresponding to vertices 1 and 3 having higher weighting than 2, 4 and 5.

References