Phonon excitations of a driven superfluid in a tilted optical lattice

Motivation

Tilted optical lattices have been used as a system to investigate intriguing physical phenomena such as Bloch oscillations, quantum tunneling, and interference. The tilt of the lattice potential can suppress tunnelling between adjacent lattice sites. However, tunnelling can then be restored by the introduction of periodic driving with a frequency that matches the energy offset of neighbouring sites. This approach has recently been used to realise artificial gauge fields in cold atom experiments.

While the tilt alone can cause instabilities in interacting systems, the addition of periodic driving introduces a complex interplay between the driving frequency and the energy offset, leading to new types of instabilities. Understanding these instabilities is crucial for selecting parameters that prevent the system from becoming excited, and enable the study of the systems over long time intervals.

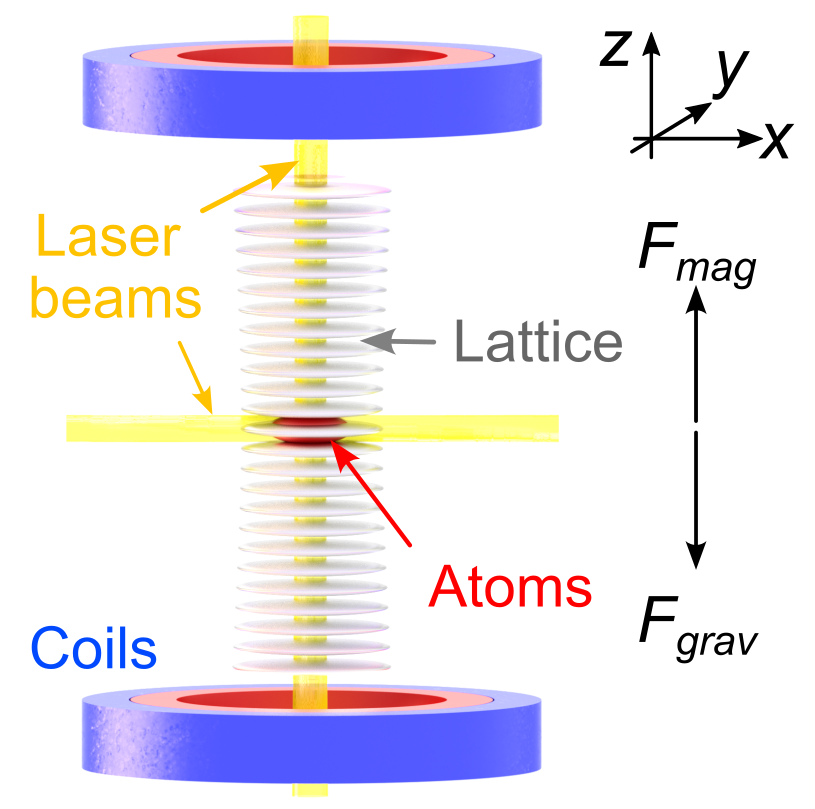
Fig. 1: Experimental setup. A Bose-Einstein condensate of cesium atoms is trapped in a vertical optical lattice and levitated using a magnetic field gradient. The driving force is applied by periodically shaking the lattice sites, and the tilt is introduced by slightly reducing the magnetic field gradient below the value required for levitation.

Fig. 1: Experimental setup. A Bose-Einstein condensate of cesium atoms is trapped in a vertical optical lattice and levitated using a magnetic field gradient. The driving force is applied by periodically shaking the lattice sites, and the tilt is introduced by slightly reducing the magnetic field gradient below the value required for levitation.

We experimentally investigated the stability of a superfluid in three separate settings:

  1. Only a static force, $F_B$.
  2. A resonant driving force where the driving frequency matches the tilt, $\hbar \omega = F_B d_L$.
  3. Off-resonant driving with detuning $\Delta \omega$.

1. Static force $F_B$

In a system with a static tilt, instabilities always arise because the superfluid’s micromotion traverses the complete Brillouin zone, inevitably entering unstable regions. In those regions at the edge of the Brillouin zone, the superfluid’s effective mass is negative, resulting in effectively attractive interaction and modulational instabilities.

Fig. 2: Instabilities due to Bloch oscillations. (a) Absorption images of the superfluid in momentum space as it is accelerated by a constant force. (b) Micromotion for constant force (black line). Phonon modes (blue circles) grow whenever the superfluid is close to the edge of the Brillouin zone (red patches).

Fig. 2: Instabilities due to Bloch oscillations. (a) Absorption images of the superfluid in momentum space as it is accelerated by a constant force. (b) Micromotion for constant force (black line). Phonon modes (blue circles) grow whenever the superfluid is close to the edge of the Brillouin zone (red patches).

We measured the growth of phonon modes over approximately 30ms for varying driving strength and lattice depths. Strong growth of phonon modes can be associated with resonances, when the driving frequency $\omega$ matches to twice the average phonon energy $\braket{E_q}$.

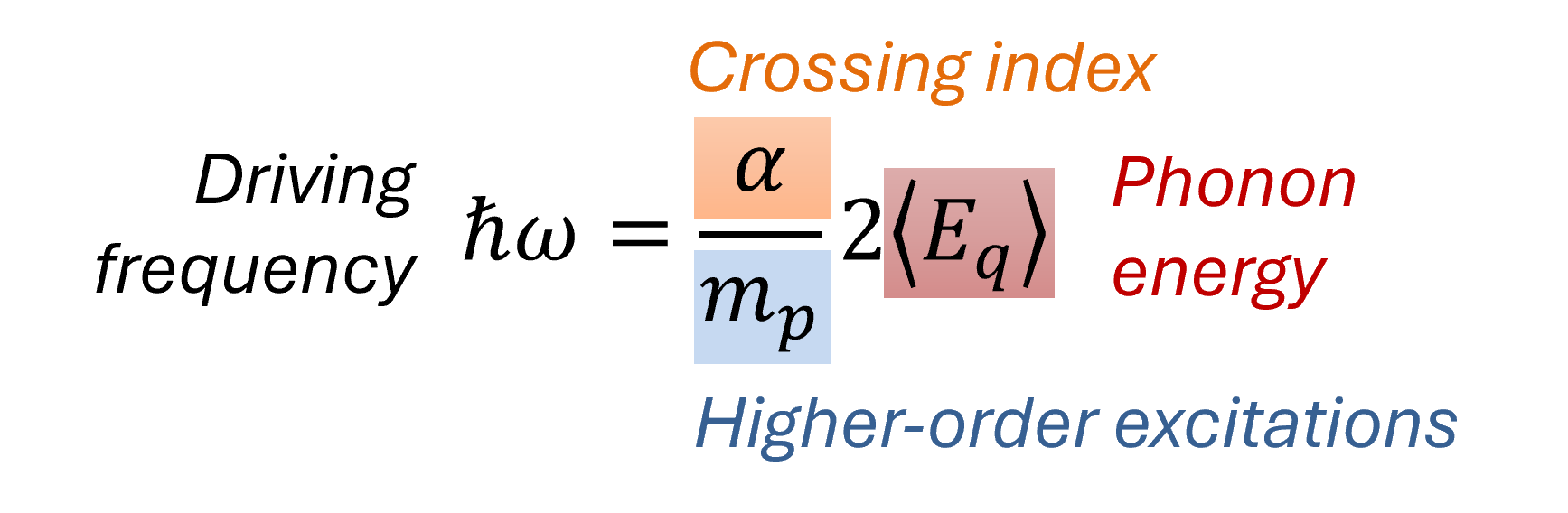
The parameter $\alpha$ indicates the relative time interval between consecutive crossings, while $m_p$ is an integer number counting higher-order excitations. We find this resonance condition to be sufficiently general to predict resonances with and without lattice tilt, and with and without driving.

2. Resonant driving, $\hbar \omega = F_B d_L$

In a second experiment, we investigated the stability for driving frequencies that resonantly match the tilt. In this system, the driving reintroduces tunneling between lattice sites regardless of the tilt’s strength. Although this system is less stable than without a tilt [Phys. Rev. Research 5, 033024 (2023)], it still exhibited parameter regimes of strong stability. We discovered that the stability heavily depends on the number of times the superfluid’s micromotion crosses in and out of unstable regions of the Brillouin zone, as captured by the $\alpha$-parameter in the resonance condition. Our results [Fig. 3(a)] were also compared to numerical simulations using the Bogoliubov-de Gennes equations [Fig. 3(b)].

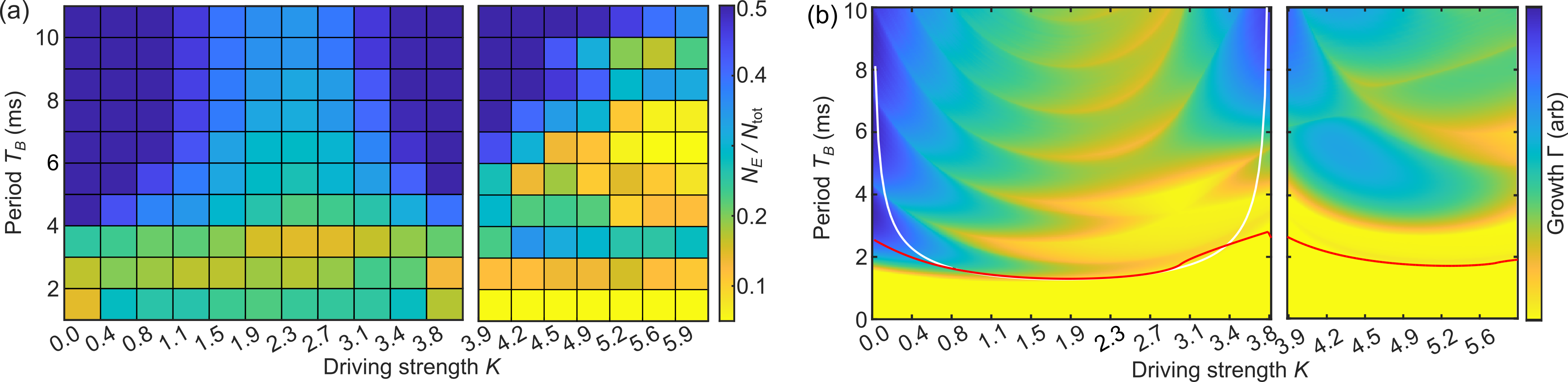
Fig. 3: Instabilities for resonant driving. (a) Measured growth of phonon modes after 30ms for various driving strengths and driving periods. (b) Calculated growth rate using the Bogoliubov-de Gennes equations.

Fig. 3: Instabilities for resonant driving. (a) Measured growth of phonon modes after 30ms for various driving strengths and driving periods. (b) Calculated growth rate using the Bogoliubov-de Gennes equations.

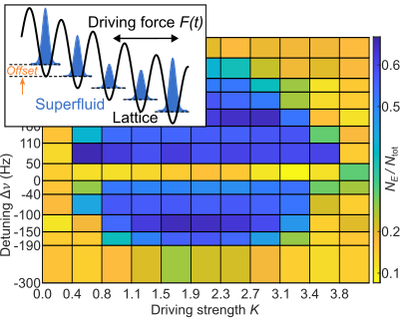
3. Off-resonant driving with detuning $\Delta \omega$

In the final experiment we changed the driving frequency while keeping the tilt constant. As a result, the superfluid showed Super-Bloch oscillations with the frequency $\Delta \omega$, which is the detuning between the frequencies of driving and Bloch oscillations. We chose a tilt frequency which was in the fast driving regime, meaning that the system was by default stable and any instabilities could be seen as arising from the detuning. The micromotion had a complicated shape that gradually shifted from predominantly stable to predominantly unstable time intervals. For small values of $\Delta \omega$, the phonon modes increased in the predominantly unstable time intervals [line and red patches in Fig. 4(a)], while the system became completely stable for large detuning with a fast alternation of stabile and unstable time intervals [Fig. 4(b)].

Fig. 4: Micromotion and growth of phonon modes for off-resonant driving. (a) Micromotion for small detuning (gray line). The phonon modes grow (circles) in predominantly unstable time intervals (red patches). (b) Micromotion for large detuning (gray line). Unstable and stable regions alternate quickly and the system is stable.

Fig. 4: Micromotion and growth of phonon modes for off-resonant driving. (a) Micromotion for small detuning (gray line). The phonon modes grow (circles) in predominantly unstable time intervals (red patches). (b) Micromotion for large detuning (gray line). Unstable and stable regions alternate quickly and the system is stable.

We adjusted the resonance condition from above for the case of Super-Bloch oscillations ($\alpha=1$) and added two integer numbers to the equation to describe tunneling to sites at distance $n_t$ and higher-order tunneling resonances $n_p$.


This condition correctly predicted phonon resonances for our measurements and for the calculated stability diagram in Fig. 5. Unstable regions appear close to tunneling resonances $n_t/n_p$, e.g. for the rations 1/2, 1/3, 1/4, 2/3, 2/5 in Fig. 5.

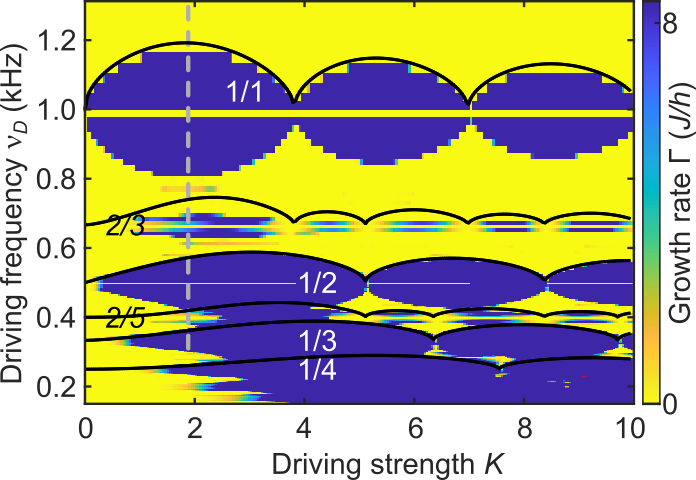
Fig. 5: Calculated growth rate of phonon modes using the Bogoliubov-de Gennes equations.

Fig. 5: Calculated growth rate of phonon modes using the Bogoliubov-de Gennes equations.

For more information, please see Phys. Rev. Research 6, 023323 (2024).