Instabilities of driven matter waves with interactions
Motivation
Optical lattices with periodically modulated driving forces provide precise control over the tunneling and band structures to create tailored lattice potentials for quantum simulation. However, simulating interacting systems in those Floquet-driven lattice potentials is challenging. Interactions can create instabilities and heating on short timescales, which are comparable to the modulation period and which quickly destroy the coherence of the system. To prevent this, it is crucial to develop an understanding of excitation mechanisms and to find an optimal window for the driving frequency.

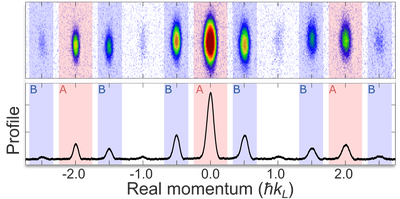
Example for growing excitation modes: A wave packet, which is initially centred at zero momentum, quickly spreads over the complete Brillouin zone due to interactions and periodic driving. Those instabilities make quantum simulation experiments challenging.
Approach
We experimentally investigate the stability of a quantum gas with repulsive interactions in an optical 1D lattice subjected to periodic driving. Excitations of the gas in the lowest lattice band are analyzed across the complete stability diagram, from slow to fast driving frequencies and from weak to strong driving strengths. To interpret our results, we expand the established analysis based on parametric instabilities to include modulational instabilities. Extending the concept of modulational instabilities from static to periodically driven systems provides a convenient mapping of the stability in a static system to the cases of slow and fast driving. At intermediate driving frequencies, we observe an interesting competition between modulational and parametric instabilities. We experimentally confirm the existence of both types of instabilities in driven systems and probe their properties. Our results allow us to predict stable and unstable parameter regions for the minimization of heating in future applications of Floquet driving.

Experimental measurement of the stability of a driven BEC in a 1D lattice potential. The number of atoms NA close to the initial quasimomentum of the quantum gas is measured after driving for approximately 30ms with strength K and driving period TD. Colors from yellow to blue indicate stable to unstable regions. Left and right panels indicate different initial states for positive and negative values of the effective tunneling element.

Numerical simulation of the growth rate of phonon modes by solving the Bogoliubov-de Gennes equations.
For more information, please see Phys. Rev. Research 5, 033024 (2023).