Motivation

Atoms can show attractive or repulsive interactions when they collide. But can atoms be both attractive and repulsive at the same time, e.g. attractive on the left side and repulsive on the right side?

The answer is: yes they can. The wave function of an ultracold atoms can be very large, extending over 100s of micrometers. We are used to the fact that the wave function adapts locally to a varying potential energy over this distance. Surprisingly, the same is true for its scattering properties, which can also vary locally over the extend of the wave function. The concept of an atom with locally changing interactions is only counterintuitive when we think of atoms as point like objects that crash into each other. A description using matter waves with fluid-like properties is well-suited to analyze those so called ‘‘collisionally inhomogeneous’’ systems.

Project summary

Collisionally inhomogeneous fluids exhibit spatially varying interactions between their particles. They frequently occur at interfaces, where interaction properties change due to a variation of an external potential or due to a change of the fluid’s composition. Examples for fluids at interfaces with a collisional inhomogeneity are liquid-vapour surfaces, and material junctions in condensed-matter physics.

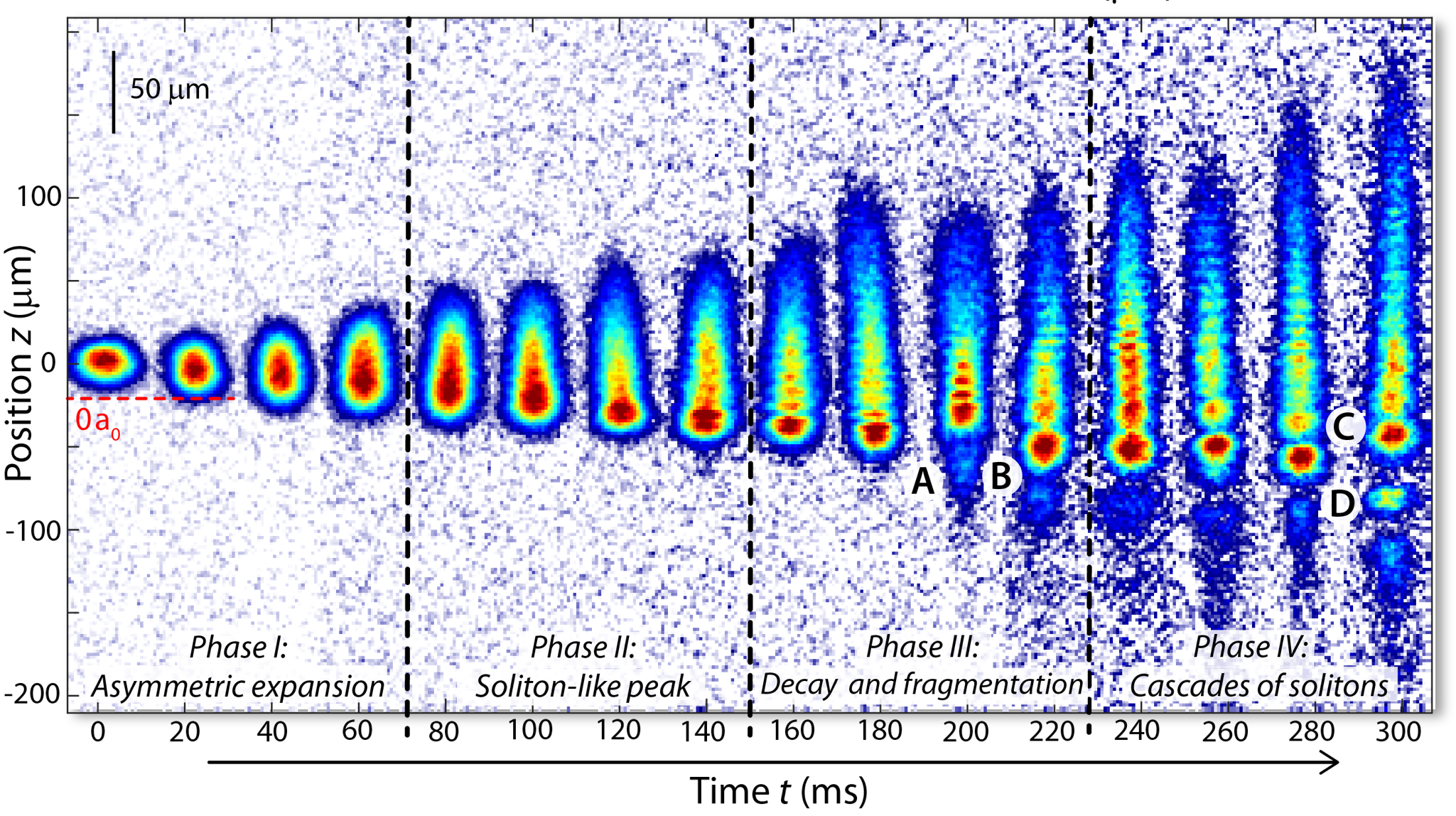
We studied the evolution of matter waves for the simplest case, i.e. a spatial gradient of the interaction strength. Starting with a Bose-Einstein condensate with weak repulsive interactions in quasi-one-dimensional geometry, we monitored the evolution of a matter wave that simultaneously extends into spatial regions with attractive and repulsive interactions. We observed the formation and the decay of soliton-like density peaks, counter-propagating self-interfering wave packets, and the creation of cascades of solitons.

The matter-wave dynamics was well reproduced in numerical simulations based on the non-polynomial Schroedinger equation with three-body loss, allowing us to better understand the underlying behavior based on a wavelet transformation [Phys. Rev. Lett. 125, 183602 (2020)].